Question

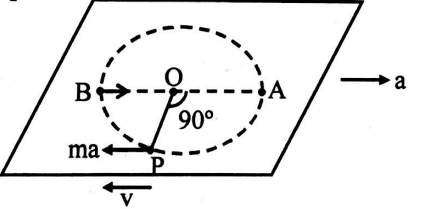
A massive horizontal platform is moving horizontally with a constant acceleration of $10\, m / s ^{2}$ as shown in the figure. A particle $P$ of mass $m =1 \,kg$ is kept at rest at the smooth surface as shown in the figure. The particle is hinged at $O$ with the help of a massless rod $OP$ of length $0.9\, m$. Hinge $O$ is fixed on the platform and the rod can freely rotate about point $O$. Now the particle $P$ is imparted a velocity in the opposite direction of the platform's acceleration such that it is just able to complete the circular motion about point $O$. Then the maximum tension appearing in the rod during the motion is $10\,n$. Find the value of $n$.

Answer 1

Relative to plate velocity imparted to particle is $V$.

$0-\frac{1}{2} m v^{2} =-m a \ell $
$v^{2} =2 a \ell$
Tension is maximum at point $B$
$T - ma =\frac{ mv _{1}^{2}}{\ell}$
$T = ma +\frac{ mv _{1}^{2}}{\ell} $
$ma \ell =\frac{1}{2} mv _{1}^{2}-\frac{1}{2} mv ^{2}$
$\frac{1}{2} mv _{1}^{2}= ma \ell+\frac{1}{2} m \times 2 a \ell$
$v _{1}^{2}=4 a \ell$
$T = ma +\frac{ m }{\ell} \times 4 a \ell$
$T =5 ma =5 \times 1 \times 10=50\, N$