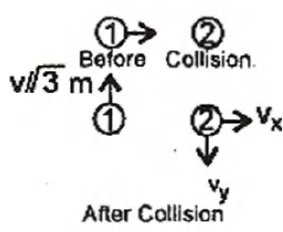
Q. A mass $'m'$ moves with a velocity $'v'$ and collides inelastically with another identical mass. After collision the $1^{st}$ mass moves with velocity $\frac{v}{\sqrt{3}}$ a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision :
AIEEEAIEEE 2005Work, Energy and Power
Solution:
In $x$-direction
$mu_1 + 0 = 0+ mv_x$
$\Rightarrow mv=mv_{x}$
$\Rightarrow v_{x}=v$
In $y$-direction
$0+0=m\left(\frac{v}{\sqrt{3}}\right)$
$\therefore $ Velocity of second mass after collision
$v'=\sqrt{\left(\frac{v}{\sqrt{3}}\right)^{2}+v^{2}}=\sqrt{\frac{4}{3}\,v^{2}}$
$\therefore v '=\frac{2}{\sqrt{3}}\,v $