Question

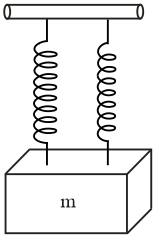
A mass $m$ is suspended separately by two different springs of spring constant $K_{1}$ and $K_{2}$ gives the time-period $t_{1}$ and $t_{2}$ respectively. If same mass $m$ is connected by both springs as shown in figure then time-period $t$ is given by the relation

• A. $t=t_{1}+t_{2}$
• B. $t=\frac{t_{1} \cdot t_{2}}{t_{1} + t_{2}}$
• C. $t^{2}=t_{1}^{2}+t_{2}^{2}$
• D. $t^{- 2}=t_{1}^{- 2}+t_{2}^{- 2}$

Answer 1

Answer: (D)

$t_{1}=2\pi \sqrt{\frac{m}{K_{1}}}$ and $t_{2}=2\pi \sqrt{\frac{m}{K_{2}}}$
Equivalent spring constant for shown combination is
$K_{1}+K_{2}.$ So time period $t$ is given by $t=2\pi \sqrt{\frac{m}{K_{1} + K_{2}}}$
By solving these equations we get $t^{- 2}=t_{1}^{- 2}+t_{2}^{- 2}$