Q.
A mass $m$ is supported by a massless string wound around a uniform hollow cylinder of mass $m$ and radius $R$. If the string does not slip on the cylinder, then with what acceleration will the mass release?
(Assume $g$ = acceleration due to gravity)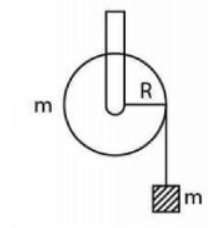
TS EAMCET 2020
Solution: