Question

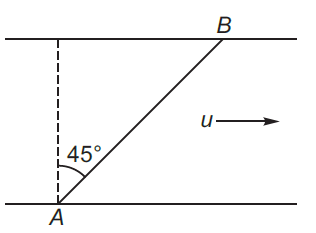
A man wants to reach point $B$ on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point $B ?$

• A. $u \sqrt{2}$
• B. $u / \sqrt{2}$
• C. 2 u
• D. u/2

Answer 1

Answer: (B)

Let $v$ be the speed of boatman in still water.

Resultant of $v$ and $u$ should be along $A B$. Components of $v _{b}$ (absolute velocity of boatman) along $x$ and $y$ directions are,
$v_{x}=u-v \sin \theta$
and $v_{y}=v \cos \theta$
Further, $\tan 45^{\circ}=\frac{v_{y}}{v_{x}}$
Or $1=\frac{v \cos \theta}{u-v \sin \theta}$
$v=\frac{u}{\sin \theta+\cos \theta}=\frac{u}{\sqrt{2} \sin \left(\theta+45^{\circ}\right)}$
$v$ is minimum at,
$\theta+45^{\circ}=90^{\circ}$ or $\theta=45^{\circ}$
and $v_{\min }=\frac{u}{\sqrt{2}}$