Q. A man standing on a horizontal plane, observes the angle of elevation of the top of a tower to be $\alpha $ . After walking a distance equal to double the height of the tower, the angle of elevation becomes $2\alpha $ , then $\alpha $ is:-
NTA AbhyasNTA Abhyas 2022
Solution:
Let $PQ$ be the tower of height $h$ .
Given, $AB=2h$ , $\angle PAQ=\alpha $ and $\angle PBQ=2\alpha $
$\therefore \angle APB=\angle PBQ-\angle PAQ=2\alpha -\alpha $
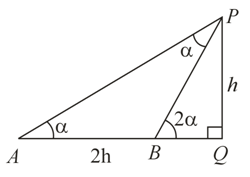
In $\Delta ABP,\angle BAP=\angle APB=\alpha $
$\therefore PB=AB=2h$
In $\Delta PQB$ ,
$sin2\alpha =\frac{P Q}{P B}=\frac{h}{2 h}=\frac{1}{2}$
$\Rightarrow sin2\alpha =sin\frac{\pi }{6}$
$\therefore 2\alpha =\frac{\pi }{6}$
$\Rightarrow \alpha =\frac{\pi }{12}$
Given, $AB=2h$ , $\angle PAQ=\alpha $ and $\angle PBQ=2\alpha $
$\therefore \angle APB=\angle PBQ-\angle PAQ=2\alpha -\alpha $

In $\Delta ABP,\angle BAP=\angle APB=\alpha $
$\therefore PB=AB=2h$
In $\Delta PQB$ ,
$sin2\alpha =\frac{P Q}{P B}=\frac{h}{2 h}=\frac{1}{2}$
$\Rightarrow sin2\alpha =sin\frac{\pi }{6}$
$\therefore 2\alpha =\frac{\pi }{6}$
$\Rightarrow \alpha =\frac{\pi }{12}$