1. Tardigrade
  2. Question
  3. Physics
  4. A man is walking due east at the rate of 2 km/h. The rain appears to him to come down vertically at the rate of 2 km/h. The actual velocity and direction of rainfall with the vertical respectively are

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

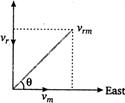
Q. A man is walking due east at the rate of 2 km/h. The rain appears to him to come down vertically at the rate of 2 km/h. The actual velocity and direction of rainfall with the vertical respectively are

EAMCETEAMCET 2008Motion in a Plane

Solution:

Velocity of man, $ {{v}_{m}}=2\,km/h $ Velocity of rain, $ {{v}_{r}}=2\,km/h $ Then actual velocity $ {{v}_{rm}}=\sqrt{v_{m}^{2}+v_{r}^{2}} $ $ =\sqrt{{{(2)}^{2}}+{{(2)}^{2}}} $ $ =\sqrt{4+4}=2\sqrt{2}\,km/h $ The direction of rainfall with the vertical
$ \sin \theta =\frac{{{v}_{r}}}{{{v}_{rm}}} $ $ =\frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}} $ $ \theta ={{\sin }^{-1}}\left( \frac{1}{\sqrt{2}} \right) $ $ \theta ={{45}^{o}} $

Solution Image