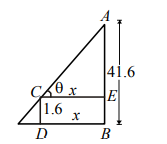
Question

A man is moving away from a tower $41.6 \,m$ high at a rate of $2 \,m / s$. If the eye level of the man is $1.6\, m$ above the ground, then the rate at which the angle of elevation of the top of the tower changes, when he is at a distance of $30\, m$ from the foot of the tower, is

• A. $-\frac{4}{125} rad / s$
• B. $-\frac{2}{25} rad / s$
• C. $-\frac{1}{625} rad / s$
• D. None of these

Answer 1

Answer: (A)

Let $C D$ be the position of man at any time $t$.
Let $B D$ be $x$. Then $E C=x$.
Let $\angle A C E$ be $\theta$.
Given $A B=41.6 \,m , C D=1.6 \,m$,
and $\frac{d x}{d t}=2 \,m / s$
$A E=A B-E B=A B-C D$
$=41.6-1.6=40 \,m$
We have to find $\frac{d \theta}{d t}$ when $x=30\, m$.
From $\triangle A E C, \tan\, \theta=\frac{A E}{E C}=\frac{40}{x}$
Differentiating w.r.t. to $t$,
$ \sec ^{2} \theta \frac{d \theta}{d t}=\frac{-40}{x^{2}} \frac{d x}{d t}$
or $\sec ^{2} \theta \frac{d \theta}{d t}=\frac{-40}{x^{2}} \times 2$
or $\frac{d \theta}{d t}=\frac{-80}{x^{2}} \cos ^{2} \theta$
$=-\frac{80}{x^{2}} \frac{x^{2}}{x^{2}+40^{2}}=-\frac{80}{x^{2}+40^{2}} .$
When $x=30\, m$,
$ \frac{d \theta}{d t}=-\frac{80}{30^{2}+40^{2}}$
$=-\frac{4}{125} rad / s$