Q.
A man in a car at location $Q$ on a straight highway is moving with speed $v$. He decides to reach a point $P$ in a field at a distance d from the highway (point $M$) as shown in the figure. Speed of the car in the field is half to that on the highway. What should be the distance $RM$, so that the time taken to reach $P$ is minimum ?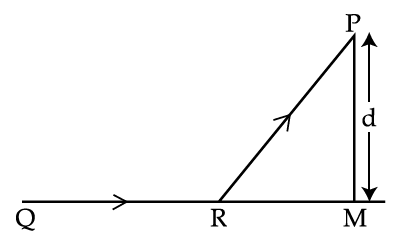
Solution:
