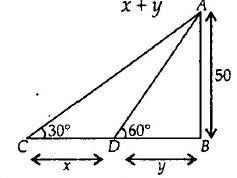
Q. A man from the top of a 50 metre high tower sees a car moving towards a tower at an angle of depression $30°$. After sometime, the angle of depression is $60°$. Then the distance travelled by the car during the time is
Solution:
In $\Delta \, ABC,$ we have $\tan 30° = \frac{50}{x+y} \frac{1}{\sqrt{3}} = \frac{50}{x+y} \, \, \, $...(i)
In $\Delta ABD,$ we have $ \tan 30° = \frac{50}{x+y}$
$\Rightarrow \sqrt{3} = \frac{50}{y} \Rightarrow y= \frac{50}{\sqrt{3} } \Rightarrow \frac{1}{\sqrt{3}} = \frac{50}{x+\frac{50}{\sqrt{3}}} $
$\Rightarrow \frac{1}{\sqrt{3}} = \frac{50\sqrt{3}}{\sqrt{3} x +50} \Rightarrow \sqrt{3} x +50 = 50 \times3$
$ \Rightarrow x = \frac{100}{\sqrt{3}} m\qquad$