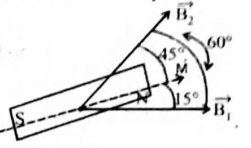
Question

A magnetic dipole is under the influence of two magnetic fields The angle between the field directions is $60^{\circ}$ and one of the fields has a magnitude of $1.2 \times 10^{-2} T$. If the dipole comes to stable equilibrium at an angle of $15^{\circ}$ with this field, what is the magnitude of other field?

• A. $4.4 \times 10^{-3}$ tesla
• B. $5.2 \times 10^{-3}$ tesla
• C. $3.4 \times 10^{-3}$ tesla
• D. $7.8 \times 10^{-3}$ tesla

Answer 1

Answer: (A)

Given that: $B _1=1.2 \times 10^{-2} T$, orientation of dipole with the field $B _1, \theta_1=15^{\circ}$
Hence, orientation of dipole with $B _2$,
$\theta_2=60^{\circ}-15^{\circ}=45^{\circ}$ (figure)
As the dipole is in equilibrium, therefore, the torque on the dipole due to the two fields must be equal and opposite.
If $M$ be the magnetic dipole moment of the dipole, then
$\tau_1=\tau_2 $
or$ MB _1 \sin \theta_1= MB _2 \sin \theta_2 $
or, $B _2=\frac{ B _1 \sin \theta_1}{\sin \theta_2}=\frac{1.2 \times 10^{-2} \sin 15^{\circ}}{\sin 45^{\circ}} $
$=\frac{1.2 \times 10^{-2} \times 0.2588}{0.7071}=4.4 \times 10^{-3}$ Tesla