Q.
A long wire having a semicircular loop of radius $r$ carries a current $i$ as shown in figure. The magnetic induction at the center $O$ due to entire wire is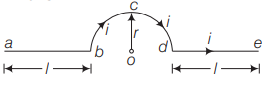
AIIMSAIIMS 2017
Solution:

Solution: