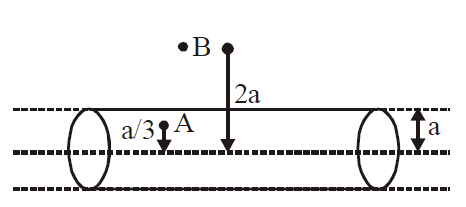
Q. A long, straight wire of radius a carries a current distributed uniformly over its cross-section. The ratio of the magnetic fields due to the wire at distance $\frac{a}{3}$ and $2a$, respectively from the axis of the wire is :
Solution:
Let current density be $J$.
$\therefore $ Applying Ampere's law.
$\oint \vec{B}.d\vec{\ell}=\mu_{0}i \Rightarrow B_{A}\,2\pi \frac{a}{3} \mu_{0}\,J\pi\left(\frac{a}{3}\right)^{2}$
$\therefore B_{A}=\frac{\mu_{0}\,Ja}{6}$
Similarly, $B_{B}=\frac{\mu_{0}\,Ja}{4}$
$\therefore \frac{B_{A}}{B_{B}}=\frac{\mu_{0}\,Ja\times4}{\mu_{0}\,J6a}=\frac{2}{3}$