Question

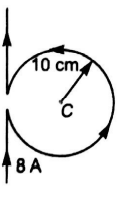
A long, straight wire is turned into a loop of radius $10\, cm$ (see figure). If a current of $8 \,A$ is passed through the loop, then the value of the magnetic field and its direction at the centre $C$ of the loop shall be close to

• A. $5.0 \times 10^{-5} \,NA ^{-1} \,m ^{-1}$, upwards
• B. $3.4 \times 10^{-5}\, NA ^{-1} \,m ^{-1}$, upwards
• C. $1.6 \times 10^{-5} \,NA ^{-1}\, m ^{-1}$, downwards
• D. $1.6 \times 10^{-5}\, NA ^{-1}\, m ^{-1}$, upwards

Answer 1

Answer: (B)

Magnetic field $B$ at the centre of a coil carrying a current, $I$ is
$B_{\text {coil }}=\frac{\mu_{0} I}{2 r}$ (upwards)
$B$ due to wire, $B_{\text {wire }}=\frac{\mu_{0} I}{2 \pi r}$ (downwards)
Magnetic field at centre $C$,
$B_{C}=B_{\text {coil }}+B_{\text {wire }}$
$=\frac{\mu_{0} I}{2 r}$ (upward) $+\frac{\mu_{0} I}{2 \pi r}$ (downwards)
$=\frac{\mu_{0} I}{2 r}-\frac{\mu_{0} I}{2 \pi r}=\frac{\mu_{0} I}{2 r}\left[1-\frac{1}{\pi}\right]$ upwards
Given $I=8 A, r=10 \times 10^{-2} m$
$=\frac{4 \pi \times 10^{-7} \times 8}{2 \times 10 \times 10^{-2}}\left[1-\frac{1}{3.14}\right]$ upwards
$=3.424 \times 10^{-5}$ upwards