Q.
A long straight wire carries a current, $I =2$ ampere. A semi-circular conducting rod is placed beside it on two conducting parallel rails of negligible resistance. Both the rails are parallel to the wire. The wire, the rod and the rails lie in the same horizontal plane, as shown in the figure. Two ends of the semi-circular rod are at distances $1 \,cm$ and $4 \,cm$ from the wire. At time $t =0$, the rod starts moving on the rails with a speed $v =3.0\, m / s$ (see the figure)
A resistor $R =1.4 \,\Omega$ and a capacitor $C _{0}=5.0\, \mu F$ are connected in series between the rails. At time $t =0, C _{0}$ is uncharged. Which of the following statement(s) is(are) correct? $\left[\mu_{0}=4 \pi \times 10^{-7} SI\right.$ units. Take $\left.\ell n 2=0.7\right]$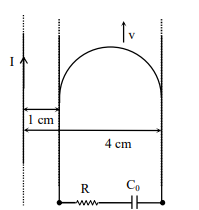
JEE AdvancedJEE Advanced 2021
Solution: