Question

A long horizontal rod has a bead which can slide along its length and is initially placed at a distance $L$ from one end $A$ of the rod. The rod starts from rest in angular motion about $A$ with a constant angular acceleration $\alpha$ .If the coefficient of friction between the rod and the bead is $\mu$ and gravity is neglected then what is the time after which the bead starts slipping

• A. $\sqrt{\mu/\alpha}$
• B. $\frac{\mu}{\sqrt{\alpha}}$
• C. $\frac{1}{\sqrt{\mu \alpha }}$
• D. infinitesimal

Answer 1

Answer: (A)

Tangential force $\left(F_{t}\right)$ of the bead will be given by the normal reaction $(N)$, while centripetal force $\left(F_{c}\right)$ is provided by friction $\left(f_{r}\right)$. The bead starts sliding when the centripetal force is just equal to the limiting friction.

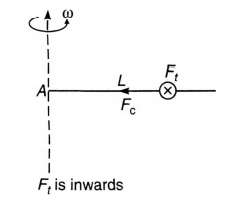
Therefore,
$ F_{t}=m a=m \alpha L=N$
$\therefore$ Limiting value of friction
$\left(f_{r}\right)_{\max }=\mu N=\mu m \alpha L ....$ (i)
Angular velocity at time $t$ is $\omega=\alpha t$
$\therefore$ Centripetal force at time $t$ will be
$F_{c}=m L \omega^{2}=m L \alpha^{2} t^{2} .....$(ii)
Equating Eqs. (i) and (ii), we get
$t=\sqrt{\frac{\mu}{\alpha}}$
For $t>\sqrt{\frac{\mu}{\alpha}}, F_{c}>\left(f_{r}\right)_{\max }$ i.e. the bead starts sliding.
In the figure, $F_{t}$ is perpendicular to the paper inwards.