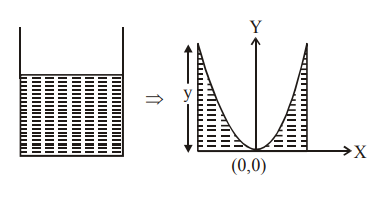
Q. A long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is $5\, cm$ and its rotational speed is $2$ rotations per second, then the difference in the heights between the centre and the sides, in $cm$, will be
Solution:
$y \, = \, \frac{\omega^2 \, x^2}{2g} \, = \, \frac{(2 \times 2\pi)^2 \times(0.05)^2}{20}] \, \, \simeq \, 2 \, cm $