Question

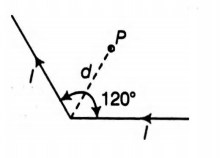
A long conducting wire carrying a current $I$ is bent at $120^{\circ}$ (see figure). The magnetic field $B$ at a point $P$ on the right bisector of bending angle at a distance d from the bend is $\left(\mu_{0}\right.$ is the permeability of free space)

• A. $\frac{3\mu_{0}I}{2\pi d}$
• B. $\frac{\mu_{0}I}{2\pi d}$
• C. $\frac{\mu_{0}I}{\sqrt{3}\pi d}$
• D. $\frac{\sqrt{3}\mu_{0}I}{2\pi d}$

Answer 1

Answer: (D)

We know that

$B_{ net }=2\left[\frac{\mu_{0} \,i}{4 \,\pi r}\left(\sin \theta_{1}+\sin \theta_{2}\right)\right]$
$=2\left[\frac{\mu_{0}}{4 \pi} \times \frac{i}{\frac{d \sqrt{3}}{2}} \times\left(\sin 90^{\circ}+\sin 30^{\circ}\right)\right.$
$=2\left[\frac{\mu_{0}}{4 \pi} \times \frac{2 i}{d \sqrt{3}} \times\left(1+\frac{1}{2}\right)\right]$
$=2\left[\frac{\mu_{0}}{4 \pi} \times \frac{2 i}{d \sqrt{3}} \times \frac{3}{2}\right]=\frac{\sqrt{3} \mu_{0} i}{2 \pi d}$