Q.
A long circular tube of length $10\, m$ and radius $0.3\, m$ carries a current I along its curved surface as shown. A wire-loop of resistance $0.005$ ohm and of radius $0.1\, m$ is placed inside the tube with its axis coinciding with the axis of the tube. The current varies as $I=I_{0} \cos (300\, t)$ where $I_{0}$ is constant. If the magnetic moment of the loop is $N \mu_{0} I _{0} \sin (300\, t )$, then $^{\circ} N '$ is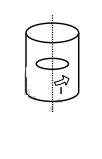
JEE AdvancedJEE Advanced 2011
Solution: