Q.
A long capillary tube of radius 1 mm open at both ends are filled with water and placed vertically. What will be the height of column of water left in capillary ? The thickness of wall of capillary is negligible. (surface tension of water $= 73.5 \times 10^{-3} N/m$ density of water $= 10^3 \,kg/m)$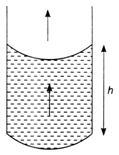
AMUAMU 2000
Solution: