Q. A load of mass $M\, kg$ is suspended from a steel wire of length $2\, m$ and radius $1.0\, mm$ in Searle's apparatus experiment. The increase in length produced in the wire is $4.0\, mm$. Now the load is fully immersed in a liquid of relative density $2$. The relative density of the material of load is $8$. The new value of increase in length of the steel wire is :
Solution:
$\frac{F}{A} \, = \, y. \frac{\Delta \ell}{\ell}$
$\Delta \ell \, \, \propto \, F \, \, \, \, \, \, \, \, \, \, \, \, $...(1)
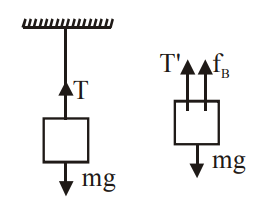
$T \, = \, mg$
$T \, = \, mg \, - \, f_B \, = \, mg \, - \, \frac{m}{\rho_b}.\rho \ell.g$
$ \, \, \, \, \, \, \, \, \, =\bigg(1 \, - \frac{\rho_\ell}{\rho_b}\bigg) mg$
$ \, \, \, \, \, \, \, \, \, \, \, \, =\bigg(1 - \frac{2}{8} \bigg) mg$
$ \, \, \, \, \, \, \, \, \, \, \, \, T' \, = \, \frac{3}{4}mg$
$From \, (1)$
$\frac{\Delta \ell'}{\Delta \ell} = \frac{T'}{T} \, = \, \frac{3}{4}$
$\Delta \ell' \, \, = \frac{3}{4} \, .\Delta \ell \, \, =3 \, mm$