Question

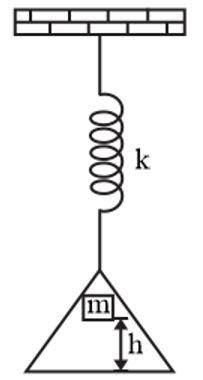
A load of mass $m$ falls from a height $h$ on to the scale pan hung from a spring, as shown in the figure. If the spring constant is $k$ , mass of the scale pan is zero and the mass $m$ does not bounce, relative to the pan, then the amplitude of vibration is

• A. $\frac{m g}{k}$
• B. $\frac{m g}{k} \, \sqrt{\left(1 + \frac{2 h k}{m g}\right)}$
• C. $\frac{m g}{k}+\frac{m g}{k} \, \sqrt{\left(\frac{1 + 2 h k}{m g}\right)}$
• D. $\frac{m g}{k} \, \sqrt{\left(\frac{1 + 2 h k}{m g} - \frac{m g}{k}\right)}$

Answer 1

Answer: (B)

According to conservation principle,
$mgh=\frac{1}{2} \, kx_{0}^{2}-mgx_{0}$
where $x_{0}$ is maximum elongation in spring (when particle is in its lowest extreme position)
or $\frac{1}{2}kx_{0}^{2}-mgx_{0}-mgh=0$
or $x_{0}^{2}-\frac{2 m g}{k} \, x_{0}-\frac{2 m g}{k} \, h=0$
$\therefore $ $x_{0}=\frac{\frac{2 m g}{k} \, \pm \, \, \sqrt{\left[\left(\frac{2 m g}{k}\right)^{2} + \, 4 \, \times \, \frac{2 m g}{k} h\right]}}{2}$
$\because $ Amplitude = elongation in spring for lowest extreme position - elongation in spring for equilibrium position $=x_{0}-x_{1}$
$=\frac{m g}{k} \, \sqrt{\left(1 + \frac{2 h k}{m g}\right)}$