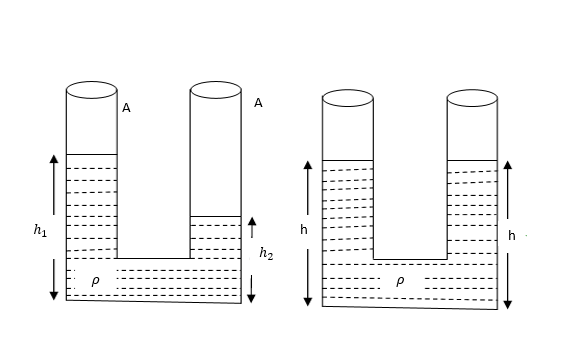
Question

A liquid of density $\rho $ is filled in two identical cylindrical vessels with base area $A$ and height of the liquid in one vessel is $h_{1}$ and that in the other vessel is $h_{2}$ . If both the vessels are connected with their base at the same level then calculate the work done by gravity in equalizing the levels.

• A. $\left(h_{1} - h_{2}\right)g\rho $
• B. $\left(h_{1} - h_{2}\right)gA\rho $
• C. $\frac{1}{2}\left(h_{1} - h_{2}\right)^{2}gA\rho $
• D. $\frac{1}{4}\left(h_{1} - h_{2}\right)^{2}gA\rho $

Answer 1

Answer: (D)

Here $h$ is the average of $h_{1}$ and $h_{2}$
So $h=\frac{h_{1} + h_{2}}{2}$
And
$\Delta h=h_{1}-h=h_{1}-\left(\frac{h_{1} + h_{2}}{2}\right)=\left(\frac{h_{1} - h_{2}}{2}\right)$
Mass of liquid displaced is
$\rho =\frac{m}{V}m=\rho Vm=\rho \times A\times \Delta hm=\rho \times A\times \left(\frac{h_{1} - h_{2}}{2}\right)$
where $\rho =$ density of liquid
$A=$ area of vessel
$V=$ volume of liquid displaced
$W=-\Delta UW=mg\Delta hW=\rho gA\times \left(\frac{h_{1} - h_{2}}{2}\right)\times \left(\frac{h_{1} - h_{2}}{2}\right)W=\frac{\rho g A}{4}\left(h_{1} - h_{2}\right)^{2}$