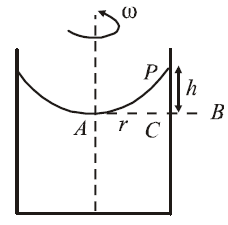
Q. A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is $r$ and angular velocity of rotation is $\omega$, then the difference in the heights of the liquid at the centre of the vessel and the edge is
Solution:
From Bernoulli’s theorem,
$P_{A}+\frac{1}{2}dv^{2}_{A}+dgh_{A}$
$=P_{_B}+\frac{1}{2}dv^{2}_{B}+dgh_{B}$
Here, $h_{A}=h_{B}$
$\therefore P_{A}+\frac{1}{2}dv^{2}_{A}=P_{B}+\frac{1}{2}dv^{2}_{B}$
$P_{A}-P_{B}=\frac{1}{2}d\left[v_{B}^{2}-v^{2}_{A}\right]$
Now, $v_{A}=0, v_{B}=r\omega$ and $P_{A}-P_{B}=hdg$
$\therefore hdg=\frac{1}{2}dr^{2} \omega^{2}$ or $h=\frac{r^{2}\omega^{2}}{2g}$