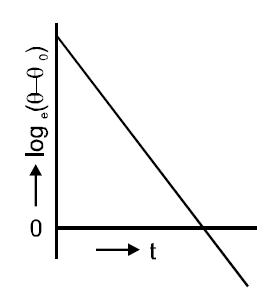
Q. A liquid in a beaker has temperature $\theta(t)$ at time $t$ and $\theta_0$ is temperature of surroundings, then according to Newton's law of cooling the correct graph between $log_{e}\left(\theta-\theta_{0}\right)$ and $t$ is :
AIEEEAIEEE 2012Thermal Properties of Matter
Solution:
$\frac{d\theta}{dt}=-k\left(\theta-\theta_{0}\right)$
$\int\limits^\theta_{{\theta_0}}$$\frac{d\theta}{\theta-\theta_{0}}=-k\int\limits^t_{{0}}dt$
$In \left(\theta-\theta_{0}\right) = -kt + C$
So graph is straight line.