Question

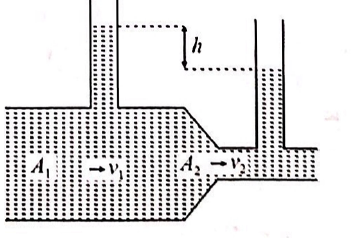
A liquid flows through a horizontal tube as shown in figure. The velocities of the liquid in the two sections, which have areas of cross-section $A_{1}$ and $A_{2}$, are $v_{1}$ and $v_{2}$, respectively. The difference in the levels of the liquid in the two vertical tubes is $h$. Then

• A. $v^{2}_{2}-v^{2}_{1}=2\,gh$
• B. $v^{2}_{2}+v^{2}_{1}=2\,gh$
• C. $v^{2}_{2}-v^{2}_{1}=gh$
• D. $v^{2}_{2}+v^{2}_{1}=gh$

Answer 1

Answer: (A)

Let $\rho$ be density of liquid flowing in the tube
$A_{1}v_{1} = A_{2}v_{2}$
$\frac{v_{1}}{v_{2}}=\frac{A_{2}}{A_{1}}$
According to Bernoullis equation for horizontal flow of liquid,
$P_{1}+\frac{1}{2} \rho v_{1}^{2}= P_{2}+\frac{1}{2} \rho v_{2}^{2}$
$P_{1}-P_{2}=\frac{1}{2}\left(\rho v_{2}^{2}-\rho v_{1}^{2}\right)$
$h\rho g=\frac{1}{2}\rho\left(v_{2}^{2}-\rho v_{1}^{2}\right)$
$h\rho g=\frac{1}{2}\rho \left(v_{2}^{2}-v_{1}^{2}\right) \,\left(\because P_{1}-P_{2}=h\rho g\right)$
$v_{2}^{2}-v_{1}^{2}=2hg$