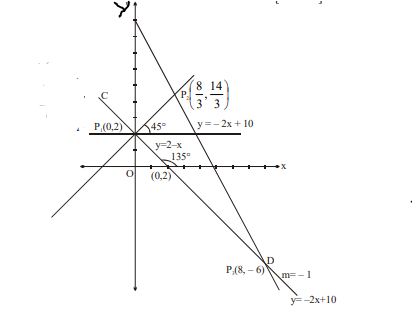
Question

A line $y=x+2$ is drawn on the co-ordinate plane. This line is rotated by $90^{\circ}$ clockwise about the point $(0,2)$. A line $y=-2 x+10$ is drawn and a triangle is formed by these three lines. If the area of the triangle is $\Delta$, then find the value $[\Delta]$ where $[ k ]$ denotes the greatest integer less than or equal to $k$.

Answer 1

Given, $y = x + 2$ .......(1)
Equation of CD
$y - 2 = - 1 (x - 0)$
$ \Rightarrow y = 2 - x$ .......(2)
Area of triangle $A B C=\frac{1}{2}\begin{vmatrix}0 & 2 & 1 \\ \frac{8}{3} & \frac{14}{3} & 1 \\ 8 & -6 & 1\end{vmatrix}$
$=\frac{1}{6}\begin{vmatrix}0 & 2 & 1 \\ 8 & 14 & 3 \\ 8 & -6 & 1\end{vmatrix}$
$ =\frac{1}{6}\begin{vmatrix}0 & 2 & 1 \\ 0 & 20 & 2 \\ 8 & -6 & 1\end{vmatrix}$
$=\frac{1}{6}|8(4-20)|=\left|\frac{8 \cdot 16}{6}\right|=\left|\frac{64}{3}\right|=\Delta $
$ \Rightarrow\left[\frac{64}{3}\right]=21 $