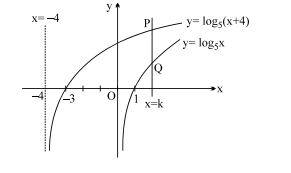
Question

A line $x=k$ intersects the graph of $y=\log _5 x$ and the graph of $y=\log _5(x+4)$. The distance between the points of intersection is 0.5 . Given $k=a+\sqrt{b}$, where $a$ and $b$ are integers, the value of $(a+b)$ is

• A. 5
• B. 6
• C. 7
• D. 10

Answer 1

Answer: (B)

Obvious $y =\log _5( x +4)$ is above $y =\log _5 x$.
Hence for $x = k , \log _5( k +4)-\log _5 k =\frac{1}{2}$

$\log _5\left(\frac{ k +4}{ k }\right)=\frac{1}{2} $
$\frac{ k +4}{ k }=\sqrt{5} $
$1+\frac{4}{ k }=\sqrt{5}$
$ k =\frac{4}{\sqrt{5}-1}=\sqrt{5}+1 \Rightarrow a =1 ; b =5 $
$\therefore a + b =6$