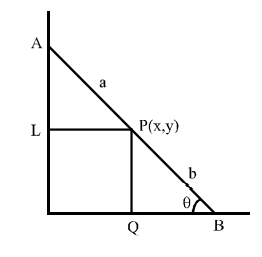
Question

A line of fixed length $a+b$ moves so that its ends are always on two fixed perpendicular straight lines. Then the locus of the point which divides this line into portions of lengths a and b is $a / an$

• A. ellipse
• B. parabola
• C. straight line
• D. none of these

Answer 1

Answer: (A)

Let $A B$ be the line.
Let $AP = a$ and $PB = b$, so the $AB = a + b$.
If $AB$ makes an angle $\theta$ with the $x$-axis and the coordinates of $P$ are $( x , y )$, then
in $\Delta APL , x = a \cos \theta$
in $\Delta PBQ , y = b \sin \theta$
Therefore, the locus of $P ( x , y )$ is
$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$
which is an ellipse.