Q.
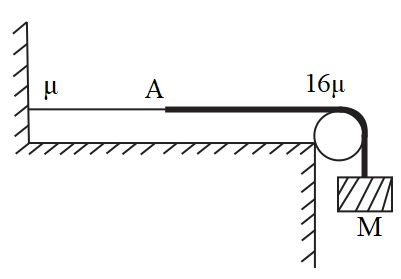
A light string is tied at one end to a fixed support and to a heavy string of equal length $L$ at the other end $A$ as shown in the figure ( Total length of both strings combined is $2L$ ). A block of mass $M$ is tied to the free end of heavy string. Mass per unit length of the strings are $\mu $ and $16\mu $ and tension is $T$ . Find lowest positive value of frequency such that junction point $A$ is a node.
NTA AbhyasNTA Abhyas 2020Waves
Solution: