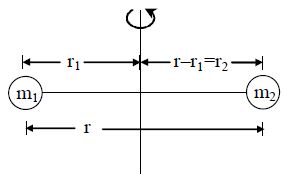
Q. A light rod of length $l$ has two masses $m_1$ and $m_2$ attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is -
Solution:
$m_{1}r_{1} = m_{2 } \left(l -r_{2}\right)$
$\left(m_{1} + m_{2}\right)r_{1} = m_{2}r $
$ r_{1} = \frac{m_{2}l}{m_{1} + m_{2}} $
and $ r_{2} =r - r_{1} = r - \frac{m_{2}l}{m_{1}+m_{2}} = \frac{m_{1}l}{m_{1} +m_{2}} $
So $ I = I_{1} + I_{2} $
$=m_{1}r_{1}^{2} + m_{2}r_{2}^{2} $
$ =m_{1} \left(\frac{m_{2}l}{m_{1}+m_{2}}\right)^{2} + m_{2}\left(\frac{m_{1}l}{m_{1}+m_{2}}\right)^{2} = \frac{m_{1}m_{2}l^{2}}{m_{1}+m_{2}}$