Q.
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses $0.36\, kg$ and $0.72\, kg$. Taking $g =10\, m / s ^{2}$, find the work done (in joules) by the string on the block of mass $0.36\, kg$ during the first second after the system is released from rest.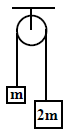
BITSATBITSAT 2013
Solution:
Given $m =0.36\, kg,\, M =0.72\, kg.$
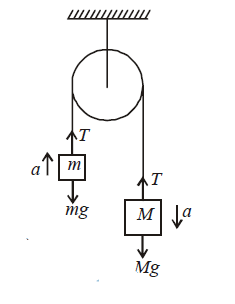
The figure shows the forces on $m$ and $M$.
When the system is released, let the acceleration be $a$. Then
Given $m =0.36\, kg,\, M =0.72\, kg$.
The figure shows the forces on $m$ and $M$.
When the system is released, let the acceleration be $a$. Then
$T=m g=m a$
$M g-T=M$
$\therefore a=\frac{(M-m) g}{M +m}=b/3$ and $T=4\, m g/3 $ (For block $m$)
$u=0, a=g/3, t=1, s=?$
$s=u t+\frac{1}{2} a t^{2}=0+\frac{1}{2} \times \frac{g}{3} \times 1^{2}=g/6$
$\therefore $ Work done by the string on $m$ is
$\vec{T} \vec{s}=T s=4 \frac{m g}{3} \times \frac{g}{6}$
$=\frac{4 \times 0.36 \times 10 \times 10}{3 \times 6}$
$=8 J$