Q.
A length of path $A C B$ is $1500\, m$ and the length of the path $A D B$ is $2100\, m$. Two particles start from point $A$ simultaneously around the track $A C B D A$. One of them travels the track in clockwise sense and other in anticlockwise sense with their respective constant speeds. After $12\, s$ from the start, the first time they meet at the point $B$. After minimum time(ins) in which they meet first at point $B$, will they again meet at the point $B$ is time $t_{\min }=(12)^{x} s$. The value of $x$ is______.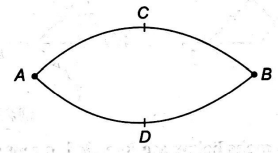
Motion in a Straight Line
Solution: