1. Tardigrade
  2. Question
  3. Physics
  4. A LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant 'b', the correct equivalence would be:

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

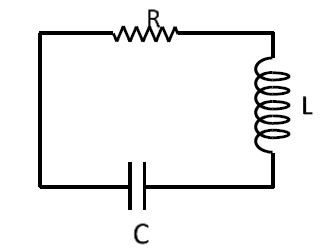
Q. A LCR circuit behaves like a damped harmonic oscillator. Comparing it with a physical spring-mass damped oscillator having damping constant 'b', the correct equivalence would be:

JEE MainJEE Main 2020Alternating Current

Solution:

In damped oscillation
$ma + bv + kx = 0$
$m=\frac{d^{2}x}{dt^{2}}+b \frac{dx}{dt}+kx=0 \,...\left(i\right)$
In the circuit
$-iR-L \frac{di}{dt}-\frac{q}{c}=0$
$L \frac{d^{2}q}{dt^{2}}+R \frac{dq}{dt}+\frac{1}{c}.q=0 \,...\left(ii\right)$
Comparing equation $\left(i\right)$ and $\left(ii\right)$
$m=L, b=R, k=\frac{1}{c}$

Solution Image