Question

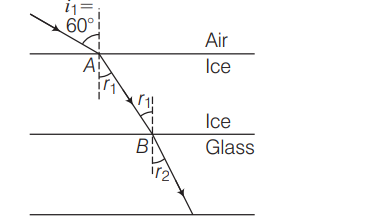
A layer of ice $(\mu=1.33)$ lies on a glass plate $(\mu=1.5)$. A ray of light makes an angle of incidence $60^{\circ}$ on the surface of ice as shown in the figure below.

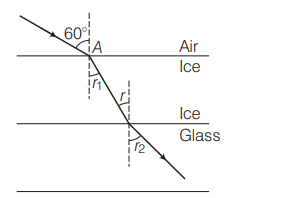
With reference to the above figure, match the items in Column I with terms in Column II and choose the correct option from the codes given below.

Column I		Column II
A	$\sin r_{1}$	1	$(1 / \sqrt{3})$
B	$\sin r_{2}$	2	$(3 \sqrt{3}) / 8$
C	Refractive Index of ice with respect to glass	3	$8 / 9$

• A. A - (1) , B - (2) , C - (3)
• B. A - (2) , B - (1) , C - (3)
• C. A - (2) , B - (3) , C - (1)
• D. A - (1) , B - (3) , C - (2)

Answer 1

Answer: (B)

In this case, the light gets refracted twice from air to ice at $A$ and from ice to glass at $B$.
We have find angle $r_{2}$. At $A$, Air-ice interface
Applying Snell's law $\frac{\sin i_{1}}{\sin r_{1}}={ }^{\text {air }} \mu_{\text {ice }}$

$\Rightarrow \frac{\sin 60^{\circ}}{\sin r_{1}}=\frac{\mu_{\text {ice }}}{1}\,\,\,...(i)$
$\Rightarrow \sin r_{1}=\frac{\sin 60^{\circ}}{\mu_{\text {ice }}}=\frac{\sqrt{3} / 2}{4 / 3}=\frac{3 \sqrt{3}}{8}\,\,\,...(ii)$
At $B$, Ice - glass interface
Applying Snell's law,
$\frac{\sin r_{1}}{\sin r_{2}}={ }^{\text {ice }} \mu_{\text {glass }}=\frac{\mu_{\text {glass }}}{\mu_{\text {ice }}}\,\,\,...(A)$
On multiplying Eqs. (i) and (ii), we get
$\frac{\sin 60^{\circ}}{\sin r_{1}} \times \frac{\sin r_{1}}{\sin r_{2}}=\frac{\mu_{\text {ice }}}{1} \times \frac{\mu_{\text {glass }}}{\mu_{\text {ice }}}$
$ \Rightarrow \frac{\sin 60^{\circ}}{\sin r_{2}}=\mu_{\text {glass }}$
$\Rightarrow \sin r_{2}=\frac{\sin 60^{\circ}}{\mu_{\text {glass }}}=\frac{(\sqrt{3 / 2})}{1.5}=\frac{\sqrt{3 / 2}}{3 / 2}=\left(\frac{1}{\sqrt{3}}\right)\,\,\,...(B)$
Also, refractive index of ice w.r.t. glass
$\Rightarrow { }^{\text {glass }} \mu_{\text {ice }}=\frac{{ }_{\text {air }} \mu_{\text {ice }}}{\text { air } \mu_{\text {glass }}}=\frac{4 / 3}{3 / 2}=\frac{8}{9}\,\,\,...(C)$