Q.
A large tank is filled with water (density = $10^{3}\, kg / m ^{3}$ ). A small hole is made at a depth $10\, m$ below water surface. The range of water issuing out of the hole is $R$ on ground. What extra pressure must be applied on the water surface so that the range becomes $2R$
(take 1 atm $=10^{5} Pa$ and $g =10\, m / s ^{2}$ )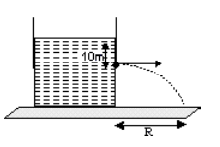
Solution: