Q.
A large spherical mass $M$ is fixed at one position and two identical point masses $m$ are kept on a line passing through the centre of $M$ (see figure). The point masses are connected by a rigid massless rod of length $I$ and this assembly is free to move along the line connecting them. All three masses interact only through their mutual gravitational interaction. When the point mass nearer to $M$ is at a distance $r = 3l$ from $M$, the tension in the rod is zero for $m = k\left(\frac{M}{288}\right)$. The value of $k$ is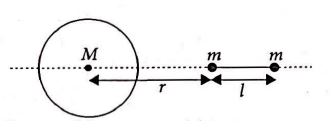
Gravitation
Solution:
