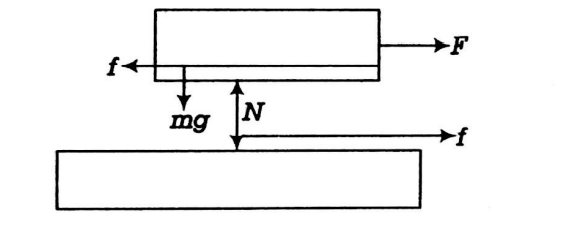
Question

A large slab of mass $5\, kg$ lies on a smooth horizontal surface, with a block of mass $4\, kg$ lying on the top of it, the coefficient of friction between the block and the slab is $0.25$. If the block is pulled horizontally by a force of $F=6 N$, the work done by the force of friction on the slab between the instants $t=2 s$ and $t=3 s$ is

• A. 2.4 J
• B. 5.55 J
• C. 4,44 J
• D. -10 J

Answer 1

Answer: (B)

Maximum frictional force between the slab and the block
$f_{\max }=\mu N=\mu mg =\frac{1}{4} \times 4 \times 10=10 N$

Evidently, $f \propto f_{\max }$
So, the two bodies will move together as a single unit.
If a be their combined acceleration, then
$a=\frac{F}{m+M}=\frac{6}{4+5}=\frac{2}{3} ms ^{-2}$
Therefore, frictional force acting can be obtained as
$f=M a=\frac{2}{3} \times 5=\frac{10}{3} N$
Using $S=\frac{1}{2} a t^{2}$
$S(2)=\frac{1}{2} \times \frac{2}{3}(2)^{2}=\frac{4}{3}$
and $S(3)=\frac{1}{2} \times \frac{2}{3} \times(3)^{2}=3$
Therefore, work done by friction $=F[S(3)-S(2)]$
$\because=\frac{10}{3}\left[3-\frac{4}{3}\right]=\frac{60}{9}=5.55 \,J$