Q.
A lamina is made by removing a small disc of diameter $2 R$ from a bigger disc of uniform mass density and radius $2 R$, as shown in the figure. The moment of inertia of this lamina about axes passing though $O$ and $P$ is $I _{0}$ and $I_{P}$ respectively. Both these axes are perpendicular to the plane of the lamina. The ratio $I_{P} / I_{O}$ to the nearest integer is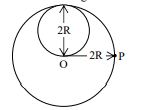
JEE AdvancedJEE Advanced 2012
Solution: