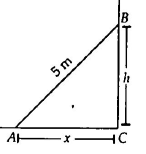
Q. A ladder $5\,m$ long is leaning against a wall. The bottom of the ladder is pulled along the ground away from the wall, at the rate of $2m/sec$. The speed at which its height on the wall decreases when the foot of the ladder is $4\, m$ away from the wall is
Solution:
Let $AB$ be the ladder of length 5 m.
We are given, $\frac{dx}{dt} = 2 \, m / sec$
In $\Delta ABC,$
$AB^2 = AC^2 + BC^2$
$\Rightarrow \:\: (5)^2 = x^2 + h^2$ ....(i)
Differentiating (i) w.r.t. t,
we get
$0 = 2x \frac{dx}{dt} + 2h \frac{dh}{dt}$
$\Rightarrow \:\:\frac{dh}{dt} = \frac{-x}{h} \frac{dx}{dt}$ .....(ii)
Now, from (i), when $x = 4$
$h^2 = 25 - 16 \:\:\: \Rightarrow \, h^2 = 9 \:\:\: \Rightarrow \:\: h = 3 \, m$
From (ii)
$\left[ \frac{dh}{dt} \right] = \frac{-4}{3} \times 2 = \frac{-8}{3}$
$\because$ The negative sign shows the height decreases and decreasing rate is $\frac{8}{3} m/sec$