Question

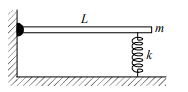
A horizontal rod of mass $m$ and length $L$ is pivoted smoothly at one end. The rod's other end is supported by a spring of force constant $k$ as shown in figure. The rod is rotated (in vertical plane) by a small angle $\theta$ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is :

• A. $\sqrt{\frac{3 k}{m}}$
• B. $\sqrt{\frac{k}{3 m}}$
• C. $\sqrt{\frac{3 k}{m}+\frac{3 g}{2 L}}$
• D. $\sqrt{\frac{k}{m}}$

Answer 1

Answer: (A)

Restoring torque on rod after small angle tilt is
$\left.\tau_{R}=-k y L=-K L^{2} \theta \text { (Since } y \cong L \theta \text { from figure }\right)$

$\Rightarrow k L^{2} \theta=-\frac{m L^{2}}{3} \cdot \alpha$
$\Rightarrow \alpha=-\frac{3 k}{m} \cdot \theta$
comparing with $\alpha=-\omega^{2} \theta$
We get $\omega=\sqrt{\frac{3 k}{m}}$
Note: Torque due to $m g$ was already balanced so it is not taken