Question

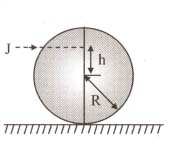
A horizontal impulse is applied at a height $h$ from the centre of a sphere initially resting on a horizontal surface. After the application of impulse, the sphere starts rolling. Compute the ratio $\frac{2 R}{h}$ .

Answer 1

Rolling is rotation about a point of contact.

Applying angular momentum equation about P,
$Mv\left(\right.R+h\left.\right)=I_{p}\omega $
As sphere rolls,
$v=\omega R$ and $I_{p}=\frac{2}{5}mR^{2}+mR^{2}=\frac{7}{5}mR^{2}$
$\therefore M\omega R\left(\right.R+h\left.\right)=\frac{7}{5}\left(MR\right)^{2}\omega $
$R+h=\frac{7}{5}R$
$\frac{R}{h}=\frac{5}{2}=2.5$
$\frac{2 R}{h}=5$