1. Tardigrade
  2. Question
  3. Physics
  4. A horizontal heavy uniform bar of weight W is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

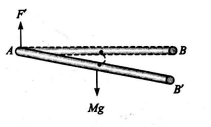
Q. A horizontal heavy uniform bar of weight $W$ is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to

System of Particles and Rotational Motion

Solution:

Let the mass of the rod is $M$
$ \Rightarrow$ Weight $(W)=M g$
Initially for the equilibrium $F+F=M g $
$\Rightarrow F=M g / 2$
image
When one man withdraws, the torque on the rod
$\tau=I \alpha=M g \frac{l}{2}$
$\Rightarrow \frac{M l^{2}}{3} \alpha=M g \frac{l}{2} \left[\right.$ As $\left.I=M l^{2} / 3\right]$
$\Rightarrow$ Angular acceleration,
$\alpha=\frac{3}{2} \frac{g}{l}$
and linear acceleration,
$a=\frac{l}{2} \alpha=\frac{3 g}{4}$
Now if the new normal force at $A$ is $F^{\prime}$ then $M g-F^{\prime}=M a$
$\Rightarrow F^{\prime}=M g-M a=M g-\frac{3 M g}{4}=\frac{M g}{4}=\frac{W}{4}$

Solution Image