Question

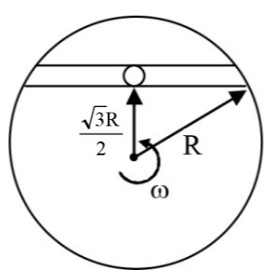
A horizontal disk is rotating with angular velocity $\omega $ about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove-

• A. $\frac{\sqrt{3}}{2}\omega R$
• B. $\frac{\omega R}{2}$
• C. $\omega R$
• D. $\frac{\omega R}{\sqrt{2}}$

Answer 1

Answer: (A)

Let us consider the motion of the ball with respect to disk


$Net \, force \, along \, groove=m\omega ^{2}r \, sin \theta $
$=m\omega ^{2}r \, \frac{x}{r}$
$=m\omega ^{2}x$
$\therefore \, ma=m\omega ^{2}x$
$\Rightarrow \, v \, \frac{d v}{d x}=\omega ^{2}x$
$\Rightarrow \displaystyle \int _{0}^{v}vdv=\displaystyle \int _{0}^{R/2}\omega ^{2}xdx$
$\Rightarrow \frac{v^{2}}{2}=\frac{\left(\omega \right)^{2}}{2}\left(\frac{R}{2}\right)^{2}$
$\Rightarrow \, v=\frac{\omega R}{2}$
$\overset{ \rightarrow }{v}_{B a l l , G r o u n d}=\overset{ \rightarrow }{v}_{B a l l , D i s k}+ \, \overset{ \rightarrow }{v}_{Disk , G r o u n d}$
$\therefore \, \left|\overset{ \rightarrow }{v}_{Ball , Ground}\right|$
$= \, \left(\left\{\left(\omega R\right)^{2} + \left(\frac{\omega R}{2}\right)^{2} + 2 \left(\omega R\right) \left(\frac{\omega R}{2}\right) cos 120 ^\circ \right\}\right)^{\frac{1}{2}}$
$=\frac{\sqrt{3}}{2}\omega R$