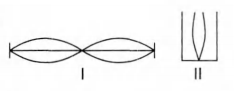
Q. A hollow pipe of length $0.8\, m$ is closed at one end. At its open end a $0.5\, m$ long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is $50\, N$ and the speed of sound is $320 \, ms^{-1}, $ the mass of the string is
IIT JEEIIT JEE 2010Waves
Solution:
Given, $2nd$ harmonic of $I =$ Fundamental of $II$
$\therefore 2 \left(\frac {v_1}{2l_1}\right)= \frac {v_2}{4l_2}$
$\Rightarrow \frac {T/\mu}{l_1}= \frac {v_2}{4l_2} $
$\Rightarrow \mu=\frac {16Tl_2^2}{v_2^2l_1^2}$
$= \frac {16 \times 50 \times (0.8)^2}{(320)^2 \times (0.5)^2 }$
$=0.02 \, kg/m $
$\therefore m_1= \mu l_1=(0.02)(0.2) $
$=0.01\,kg=10\,g$