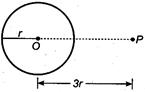
Q. A hollow charged metal sphere has a radius $r$. If the potential difference between its surface and a point at a distance $3\, r$ from the centre is $V$, then electrical intensity at distance $3\, r$ from the centre is
J & K CETJ & K CET 2003
Solution:
The potential at a distance $r$, due to charge $q$ is $V=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{r}$
Potential at a distance $(3 r)$ is
$V=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{q}{3 r}$
Difference in potential $=\frac{q}{4 \pi \varepsilon_{0}}\left[\frac{1}{r}-\frac{1}{3 r}\right]$
$\Rightarrow V=\frac{2 q}{4 \pi \varepsilon_{0} \times 3 r}$
Intensity of electric field $E=\frac{q}{4 \pi \varepsilon_{0}} \frac{1}{(3 r)^{2}}$
$\therefore \frac{E}{V}=\frac{q}{4 \pi \varepsilon_{0} q r^{2}} \times \frac{4 \pi \varepsilon_{0} 3 r}{2 q}$
$\Rightarrow \frac{E}{V}=\frac{1}{6 r}$
$\Rightarrow E=\frac{V}{6 r}$