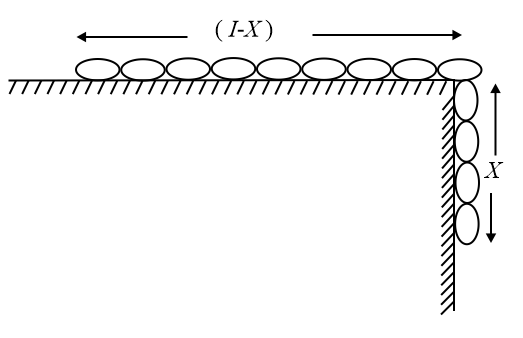
Question

A heavy uniform chain lies on a horizontal tabletop. If the coefficient of friction between the chain and the table surface is $0.25$ , then the maximum fraction of the length of the chain that can hang over one edge of the table is

• A. $20 \, \%$
• B. $25 \, \%$
• C. $35 \, \%$
• D. $15 \, \%$

Answer 1

Answer: (A)

Let the length of the chain be $l$ and mass $m$ . Let a part $x$ of the chain can hang over one edge of table having coefficient of friction $\mu $

$\therefore $ Pulling force, $F=\frac{m x}{l}g$
and friction force, $f=\mu N=\mu \frac{m}{l}\left(\right.l-x\left.\right)g$
For equilibrium, $F=f,$ hence
$\frac{m x}{l}.g=\mu \frac{m}{l}\left(l - x\right)g=0.25\frac{m}{l}\left(l - x\right)g$
$\Rightarrow \, x=\frac{l}{5}$ or $\frac{x}{l}=\frac{1}{5}=20\%$