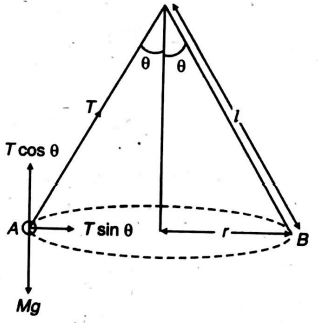
Question

A heavy small-sized sphere is suspended by a string of length L The sphere rotates uniformly in a horizontal circle with the string making an angle $ \theta $ with the vertical. Then, the time-period of this conical pendulum is

• A. $ t=2\pi \sqrt{\frac{l}{g}} $
• B. $ t=2\pi \sqrt{\frac{l\sin \theta }{g}} $
• C. $ t=2\pi \sqrt{\frac{l\cos \theta }{g}} $
• D. $ t=2\pi \sqrt{\frac{l}{g\cos \theta }} $

Answer 1

Answer: (C)

Radius of circular path in the horizontal plane
$r=l \sin \theta$

Resolving $T$ along the vertical and horizontal directions, we get
$T \,\cos\, \theta=M g \ldots$(i)
$T \,\sin \,\theta=Mr \omega^{2}=M(l \sin \theta) \omega^{2}$
or $T=M l \omega^{2} \ldots$(ii)
Dividing Eq. (ii) by Eq. (i), we get
$\frac{1}{\cos \theta}=\frac{l \omega^{2}}{g} \text { or } \omega^{2}=\frac{g}{l \cos \theta}$
$\therefore $ Time period ·
$t=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{l \cos \theta}{g}}$