Q.
A heating element of resistance $r$ is fitted inside an adiabatic cylinder which carries
a frictionless piston of mass $m$ and cross-section $A$ as shown in diagram. The cylinder contains one mole of an ideal diatomic gas. The current flows through the element such that the temperature rises with time t as $\Delta T=\alpha t+\frac{1}{2} \beta t^{2}(\alpha$ and $\beta$ are constants), while pressure remains constant. The atmospheric pressure above the piston is $P_{0}$. Then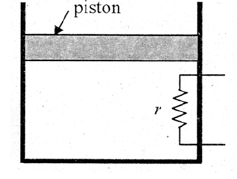
WBJEEWBJEE 2014
Solution: