Q.
A heater is operated with a power of $1000 \,W$ in a $100\, V$ line. It is connected in combination with a resistance of $10 \Omega$ and a resistance $R$ to a $100\, V$ line as shown in figure. What should be the value of $R$ so, that the heater operates with a power of $62.5$ watt.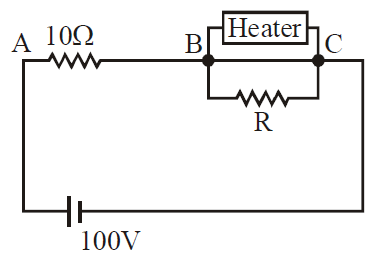
Solution: